Все уравнения плоскости, которые разобраны в следующих пунктах могут быть получены из общего уравнения плоскости, а также приведены к общему уравнению плоскости. Таким образом, когда говорят об уравнении плоскости, то имеют в виду общее уравнение плоскости, если не оговорено иное.

Уравнение плоскости в отрезках.

Уравнение плоскости вида , где a , b и c – отличные от нуля действительные числа, называется уравнением плоскости в отрезках .

Такое название не случайно. Абсолютные величины чисел a , b и c равны длинам отрезков, которые отсекает плоскость на координатных осях Ox , Oy и Oz соответственно, считая от начала координат. Знак чисел a , b и c показывает, в каком направлении (положительном или отрицательном) следует откладывать отрезки на координатных осях.

Для примера построим в прямоугольной системе координат Oxyz плоскость, определенную уравнением плоскости в отрезках . Для этого отмечаем точку, удаленную на 5 единиц от начала координат в отрицательном направлении оси абсцисс, на 4 единицы в отрицательном направлении оси ординат и на 4 единицы в положительном направлении оси аппликат. Осталось соединить эти точки прямыми линиями. Плоскость полученного треугольника и есть плоскость, соответствующая уравнению плоскости в отрезках вида .

Для получения более полной информации обращайтесь к статье уравнение плоскости в отрезках , там показано приведение уравнения плоскости в отрезках к общему уравнению плоскости, там же Вы также найдете подробные решения характерных примеров и задач.

Нормальное уравнение плоскости.

Общее уравнение плоскости вида называют нормальным уравнением плоскости , если равна единице, то есть, , и .

Часто можно видеть, что нормальное уравнение плоскости записывают в виде . Здесь - направляющие косинусы нормального вектора данной плоскости единичной длины, то есть , а p – неотрицательное число, равное расстоянию от начала координат до плоскости.

Нормальное уравнение плоскости в прямоугольной системе координат Oxyz определяет плоскость, которая удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости . Если p=0 , то плоскость проходит через начало координат.

Приведем пример нормального уравнения плоскости.

Пусть плоскость задана в прямоугольной системе координат Oxyz общим уравнение плоскости вида . Это общее уравнение плоскости является нормальным уравнением плоскости. Действительно, и нормальный вектор этой плоскости имеет длину равную единице, так как .

Уравнение плоскости в нормальном виде позволяет находить расстояние от точки до плоскости .

Рекомендуем более детально разобраться с данным видом уравнения плоскости, посмотреть подробные решения характерных примеров и задач, а также научиться приводить общее уравнение плоскости к нормальному виду. Это Вы можете сделать, обратившись к статье .

Список литературы.

• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
• Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
• Ильин В.А., Позняк Э.Г. Аналитическая геометрия.

12.1. Основные понятия

Поверхность и ее уравнение

Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О 1 есть геометрическое место всех точек пространства, находящихся от точки O 1 на расстоянии R.

Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками простран­ства и тройками чисел х, у и z - их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего ко­ординаты всех точек поверхности.

Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x, у, z) = 0 с тремя переменны­ми х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называ­ются текущими координатами точек поверхности.

Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка M 1 (x 1 ;y 1 ;z 1) на данной поверхности, достаточно подстави ть координаты точки M 1 в уравнение поверхности вместо пере­менных: если эти координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют - не лежит.

Уравнение сферы

Найдем уравнение сферы радиуса R с центром в точке O 1 (x 0 ;y 0 ;z 0). Согласно определению сферы расстояние любой ее точки М(х; у; z) от центра O 1 (x 0 ;y 0 ;z 0) равно радиусу R, т. е. O 1 M= R. Но , где . Следовательно,

Это и есть искомое уравнение сферы. Ему удовлетворяют координаты лю­бой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.

Если центр сферы Ο 1 совпадает с началом координат, то уравнение сферы принимает вид .

Если же дано уравнение вида F(x;y;z) = 0 , то оно, вообще говоря, определяет в пространстве некоторую поверхность.

Выражение «вообще говоря» означает, что в отдельных случаях уравнение F(x; y; z)=0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».

Так, уравнению не удовлетворяют никакие дей­ствительные значения х, у, z. Уравнению удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: у = 0, z = 0, а х - любое число).

Итак, поверхность в пространстве можно задать геометрически и ана­литически. Отсюда вытекает постановка двух основных задач:

1. Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.

2. Дано уравнение F(x;y;z) = 0. Исследовать форму поверхности, определяемой этим уравнением.

Уравнения линии в пространстве

Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 66) или как геометрическое место точек, об­щих двум поверхностям.

Если и - уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными:

(12.1)

Сравнения системы (12.1) называются уравнениями линии в пространстве. Например, есть уравнения оси Ох.

Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 67). В этом случае ее задают векторным уравнением

или параметрическими уравнениями

проекций вектора (12.2) на оси координат.

Например, параметрические уравнения винтовой линии имеют вид

Если точка Μ равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка Μ описывает винтовую линию (см. рис. 68).

12.2. Уравнения плоскости в пространстве

Простейшей поверхностью является плоскость. Плоскость в пространстве Oxyz можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения.

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

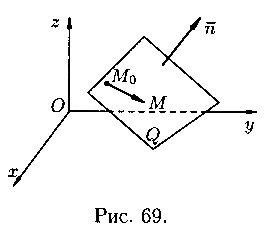
Пусть в пространстве Oxyz плоскость Q задана точкой и вектором , перпендикулярным этой плоскости (см. рис. 69). Выведем уравнение плоскости Q. Возьмем на ней произвольную точку и составим вектор . При любом расположении точки Μ на плоскости Q векторы и взаимно перпендикулярны, поэтому их скалярное произведение равно нулю: , т. е.

(12.3)

Координаты любой точки плоскости Q удовлетворяют уравнению (12.3), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют (для них ).

Уравнение (12.3) называется уравнением плоскости, проходящей через данную точку перпендикулярно вектору . Оно первой степени относительно текущих координат x, y, z. Вектор называется нормальным вектором плоскости.

Придавая коэффициентам А, В и С уравнения (12.3) различные значения, можно получить уравнение любой плоскости, проходящей череp точку . Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей, а уравнение (12.3) - уравнением связки плоскостей.

Общее уравнение плоскости

Рассмотрим общее уравнение первой степени с тремя переменными х, у и z:

Полагая, что по крайней мере один из коэффициентов А, В или С не равен нулю, например , перепишем уравнение (12.4) в виде

Сравнивая уравнение (12.5) с уравнением (12.3), видим, что уравнения (12.4) и (12.5) являются уравнением плоскости с нормальным вектором , проходящей через точку .

Итак, уравнение (12.4) определяет в системе координат Oxyz некоторую плоскость. Уравнение (12.4) называется общим уравнением плоскости.

Частные случаи общего уравнения плоскости:

1. Если D = 0, то оно принимает вид . Этому уравнению удовлетворяет точка . Следовательно, в этом случае плос­кость проходит через начало координат.

2. Если С = 0, то имеем уравнение . Нормальный вектор перпендикулярен оси Οz. Следовательно, плоскость параллельна оси Οz; если B = 0 - параллельна оси Оу, А = 0 - параллельна оси Ох.

3. Если С = D = 0, то плоскость проходит через параллельно оси Οz, т. е. плоскость проходит через ось Οz. Аналогично, уравнениям и отвечают плоскости, проходящие соответственно через оси Ох и Оу.

4. Если А = В = 0, то уравнение (12.4) принимает вид , т. е. Плоскость параллельна плоскости Оху. Аналогично, уравнениям и отвечают плоскости, соответственно параллельные плоскостям Oyz и Οxz.

5. Если A = B = D = 0, то уравнение (12.4) примет вид , т. е. z = 0. Это уравнение плоскости Оху. Аналогично: у = 0 - уравнение плоскости Οxz; x = О - уравнение плоскости Oyz.

Уравнение плоскости, проходящей через три данные точки

Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данные точки M 1 (x 1 ;y 1 ;z 1), М 2 (x 2 ;y 2 ;z 2) и М 3 (х 3 ,y 3 ,z 3), не лежащие на одной прямой.

Возьмем на плоскости произвольную точку M(x;y;z) и составим век­торы , , . Эти векторы лежат на плоскости Q, следовательно, они компланарны. Используем условие компланарнос­ти трех векторов (их смешанное произведение равно нулю), получаем , т. е.

(12.6)

Уравнение (12.6) есть уравнение плоскости, проходящей через три данные точки.

Уравнение плоскости в отрезках

Пусть плоскость отсекает на осях Ох, Оу и Оz соответственно отрезки a , b и c , т. е. проходит через три точки A(a;0;0) , B(0;b;0) и C(0;0;c) (см.рис. 70). Подставляя координаты этих точек в уравнение (12.6), получаем

Раскрыв определитель, имеем , т. е. или

(12.7)

Уравнение (12.7) называется уравнением плоскости в отрезках на осях. Им удобно пользоваться при построении плоскости.

Нормальное уравнение плоскости

Положение плоскости Q вполне определяется заданием единичного вектора , имеющего направление перпендикуляра ОК, опущенного на

плоскость из начала координат, и длиной p этого перпендикуляра (см. рис. 71).

Пусть ОК = p , а α, β, g - углы, образованные единичным вектором ё с осями Ох, Оу и Οz. Тогда . Возьмем на плоскости произвольную точку М(х; у; z) и соединим ее с началом координат. Образуем вектор . При любом положении точки Μ на плоскости Q проекция радиус-вектора на направление вектора всегда равно р: , т. е. или

(12.8)

Уравнение (12.8) называется нормальным уравнением плоскости в векторной форме. Зная координаты векторов f и e , уравнение (12.8) перепишем в виде

Уравнение (12.9) называется нормальным уравнением плоскости в координатной форме.

Отметим, что общее уравнение плоскости (12.4) можно привести к нормальному уравнению (12.9) так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части уравнения (12.4) на норми­рующий множитель , где знак берется противоположным знаку свободного члена D общего уравнения плоскости.

Раздел 5. Аналитическая геометрия.

1. Различные уравнения плоскости в пространстве

2. Частные случаи общего уравнения плоскости

3. Взаимное расположение двух плоскостей

4. Расстояние от точки до плоскости

5. Различные уравнения прямой в пространстве

6. Взаимное расположение двух прямых в пространстве

7. Взаимное расположение прямой и плоскости в пространстве

8. Различные уравнения прямой линии на плоскости

9. Геометрическая задача линейного программирования

Различные уравнения плоскости в пространстве.

В предыдущих параграфах говорилось о том, что каждой точке пространства ставится в соответствие упорядоченный набор чисел – её координаты. Естественно предположить, что если точки, обнаруживая некоторую закономерность, «выстраиваются» в виде некоторой линии или поверхности, то и их координаты также будут демонстрировать эту закономерность, удовлетворяя, как правило, некоторому уравнению, которое и называется уравнением этой линии, или поверхности.

Рассмотрим сначала пространство R 3 – реальное трёхмерное пространство (в котором мы живём). Простейшей поверхностью в пространстве является плоскость. Плоскость может быть задана различными способами, этим способам соответствуют различные формы уравнений этой плоскости. В частности, плоскость вполне

Определена, если известна какая-нибудь

M

точка М 0 , лежащая на этой плоскости

(она называется опорной ), и какой-нибудь

вектор, от которого требуется лишь одно

Рис.1 – он должен быть перпендикулярен

плоскости. Такой вектор называется вектором нормали и обычно обозначается (см. рис. 1).

Составить уравнение плоскости – значит охарактеризовать некоторым уравнением все точки плоскости. Для этого берём из этого бесчисленного множества точек любую (так сказать, представителя этого множества) и составляем для неё (т.е. для её координат) на основе замеченной закономерности уравнение. Поскольку точка была любой, то это уравнение будет справедливым и для всех точек плоскости.

Возьмём произвольную точку М (см. рис.1). Теперь образуем вектор . Ясно, что . Воспользуемся условием перпендикулярности двух векторов – их скалярное произведение равно нулю:

(1)

Уравнение (1) называют векторным уравнением плоскости. Это уравнение справедливо в любой системе координат.

Рассмотрим теперь уравнение (1) в декартовой системе координат. Пусть точка М 0 имеет координаты , координаты вектора принято обозначать: . Т.к. точка М – произвольная, её координаты: , следовательно, . Тогда формула (1) примет вид

его будем называть уравнением плоскости с опорной точкой и вектором нормали. Раскроем скобки в уравнении (2):

Обозначив, получим

Уравнение (3) называется общим уравнением плоскости. Отсюда видно, что всякое уравнение первой степени представляет собой плоскость.

Хорошо известно, что три точки однозначно определяют плоскость.

М 1

М

М 2 Пусть точки М 1 , М 2 , М 3 образуют

некоторую плоскость (т.е. не лежат

М 3 на одной прямой). Составим

уравнение этой плоскости

Рис. 2 (см. рис.2). Для этого возьмём

произвольную точку М, лежащую в плоскости и рассмотрим три вектора Поскольку М принадлежит плоскости, векторы эти компланарны, а условием компланарности трёх векторов является равенство нулю их смешанного произведения:

Уравнение (4) – ещё одно векторное уравнение плоскости, справедливое для любой системы координат. В декартовой системе координат пусть , ; тогда

И уравнение (4) выглядит следующим образом:

X – x 1 y – y 1 z – z 1

x 2 – x 1 y 2 – y 1 z 2 – z 1 = 0 (5)

x 3 – x 1 y 3 – y 1 z 3 – z 1

Уравнение (5) называют уравнением плоскости, проходящей через три точки.

Пример 1 . Написать уравнение плоскости, проходящей через точку М 0 (1,2,-3) перпендикулярно вектору

Решение . Воспользовавшись уравнением (2), получим уравнение плоскости

Заметим, что в уравнении могут отсутствовать некоторые переменные.

Пример 2 . Написать уравнение плоскости, проходящей через начало координат перпендикулярно вектору

Решение. Воспользуемся уравнением (2): Заметим, что в уравнении отсутствует свободный член (точнее, свободный член равен нулю).

Пример 3 . Написать уравнение плоскости, проходящей через три точки А(1,1,3), В(0,2,3), С(1,5,7).

Решение. Воспользуемся уравнением (5):

Вычислим определитель разложением по первой строке:

5.2. Частные случаи общего уравнения плоскости.

Возьмём общее уравнение плоскости и рассмотрим несколько его частных случаев.

1) D = 0, т.е. уравнение плоскости имеет вид

(6)

Ясно, что этому уравнению всегда удовлетворяет точка О(0,0,0) – начало координат. Итак, если в уравнении плоскости свободный член равен нулю, то плоскость проходит через начало координат.

2) С = 0, т.е. уравнение плоскости имеет вид

(7)

Это означает, что вектор нормали имеет следующие координаты Нетрудно увидеть, что - вектор нормали перпендикулярен базисному вектору , т.е. оси oz, т.к. их скалярное произведение равно нулю: Теперь понятно,

что плоскость параллельна оси oz (рис.3).

Аналогично, если В = 0, то плоскость параллельна оси ОУ; если А = 0, то плоскость параллельна оси ОХ.

Итак, если в уравнении плоскости равен нулю коэффициент при некотором неизвестном, то плоскость параллельна одноименной оси координат.

3)Пусть равны нулю два параметра – свободный член и один коэффициент, например, С = = 0. Уравнение плоскости имеет вид

(8)

Из предыдущего ясно, что С =0 означает, что плоскость параллельна оси oz, а = 0 означает, что плоскость проходит через начало координат. Объединяя оба замечания, получаем, что плоскость проходит через ось oz.

Общий вывод: если в уравнении равны нулю свободный член и коэффициент при каком-нибудь неизвестном, то плоскость проходит через соответствующую ось координат.

4) Пусть равны нулю два коэффициента при неизвестных, например А = В =0, т.е. уравнение плоскости имеет вид

. (9)

Учитываем предыдущие рассуждения: если А = 0, то плоскость параллельна оси ОХ; если В = 0, то плоскость параллельна оси ОУ, следовательно, если

А = В = 0, то плоскость параллельна осям ОХ и ОУ, т.е. перпендикулярна оси

Z ОZ и отсекает на этой оси отрезок,

D/С равный – D/С (см. рис.4).

Отсюда следует:

х = 0 – уравнение координатной плоскости yoz,

у = 0 – уравнение координатной плоскости хоz,

z = 0 – уравнение координатной плоскости уоz.

5.3. Взаимное расположение двух плоскостей.

Взаимное расположение двух плоскостей определяется с помощью угла между ними (см. рис.5. Вообще говоря, можно увидеть два угла,

которые плоскости образуют

между собой – угол и

Дополнительный угол .

Один из них – острый, другой

тупой (в случае перпендикулярности

Плоскостей оба угла совпадают).

Под углом между двумя плоскостями понимается всегда острый угол . Этот угол вычисляется с помощью угла между векторами нормалей (через скалярное произведение векторов нормалей):

(10)

На рис. 6 угол . Однако, в качестве вектора нормали к плоскости можно взять вектор . Тогда формула (10) даст косинус угла . Косинусы углов и будут отличаться лишь знаком. Поэтому, если мы хотим получить острый угол, то в формуле (10) скалярное произведение надо взять по абсолютной величине (по модулю):

(11)

Формулу (11) легко переписать в координатной форме. Пусть плоскости задаются уравнениями и . Таким образом, имеем два вектора нормалей: и По формуле (11) получим:

(12)

Теперь нетрудно получить два крайних случая: перпендикулярность и параллельность плоскостей. Если плоскости перпендикулярны, то

условие перпендикулярности плоскостей. Если плоскости параллельны, то векторы нормалей коллинеарны: , т.е. их координаты пропорциональны:

(14)

условие параллельности плоскостей.

Пример 4 . Даны три плоскости

Найти углы между этими плоскостями.

Решение . Имеем три вектора нормалей Нетрудно заметить, что , т.е. плоскости параллельны. Найдём угол между плоскостями

5.4. Расстояние от точки до плоскости.

Пусть требуется найти расстояние от

точки до плоскости.

Уравнение плоскости возьмём в виде

Уравнения с опорной точкой

И вектором нормали , т.е.

Как известно, расстояние равно длине перпендикуляра (рис. 5). Для наглядности начало вектора поместим в точку . Построим прямоугольник и увидим, что - проекции вектора на вектор нормали (см. рис. 5).

Вспоминаем определение скалярного произведения векторов:

(15)

Вновь замечаем, что на рис. 5 векторы образуют острый угол и потому является положительным числом. Если в качестве вектора нормали взять противоположный вектор (см. рис.5), то формула (15) даст отрицательное число, но расстояние есть число положительное, поэтому для расстояния d от точки до плоскости надо применять формулу

Распишем формулу (16) в координатной форме:

Скобку мы ранее обозначали буквой D. Поэтому получаем формулу

, - (17)

для нахождения расстояния от точки до плоскости заданной общим уравнением, надо в общее уравнение плоскости подставить координаты точки , поделить на длину вектора нормали и взять по модулю.

Пример 5 . Найти расстояние от точки до плоскости .

Решение . Воспользуемся формулой (17):

5.5. Различные уравнения прямой в пространстве.

Прямую линию в пространстве можно

Задать с помощью опорной точки , (т.е.

М точка лежит на прямой) и вектора , от

рис. 6 которого требуется одно – он должен

быть параллелен прямой. Такой вектор называется направляющим вектором прямой (см. рис. 6).

Для составления уравнения возьмём произвольную точку М, принадлежащую прямой, - получим вектор . Векторы и . – коллинеарны (параллельны), следовательно имеет место соотношение

где - некоторое число. Уравнение (18) называется векторным уравнением прямой. Оно будет справедливо в любом пространстве и не зависит от выбора системы координат.

Обозначим соответствующие координаты:

Тогда уравнение (18) имеет вид: или

Это обычно записывают в следующих формах:

(19)

Уравнения (19) называются параметрическими уравнениями прямой в пространстве ( - параметр).

Если из этих уравнений исключить параметр , то получим:

(20)

это так называемые канонические уравнения прямой в пространстве. От канонических легко перейти к параметрическим уравнениям прямой – достаточно все уравнения (20) приравнять параметру .

Важный для практики случай, когда прямая задаётся двумя точками , легко сводится к формуле (20), - стоит лишь заметить, что в качестве направляющего вектора можно взять вектор , а опорной точкой можно считать любую из них. Пусть тогда и опорной точкой возьмём , тогда из формулы (20) имеем:

(21)

Это уравнение называется уравнением прямой, проходящей через две точки.

5.6. Взаимное расположение двух прямых в пространстве.

Две прямые в пространстве могут

пересекаться, быть параллельными и

Скрещивающимися.

Пусть даны канонические уравнения двух прямых т.е. с опорными точками и направляющими векторами = .

Если т.е. , то прямые параллельны и даже могут совпадать. Подставим координаты опорной точки в уравнение прямой (или наоборот). Если точка лежит на прямой , то прямые совпадают, в противном случае – параллельны.

Пусть теперь т.е. векторы не параллельны (не коллинеарны). Тогда прямые могут пересекаться или скрещиваться. Как различить эти случаи? Делается это с помощью вектора (см. рис. 7). Ясно, что если прямые пересекаются, то векторы находятся в одной плоскости (точнее, они параллельны одной плоскости – компланарны). Условием компланарности векторов является равенство нулю их смешанного произведения:

(22)

Итак, если и выполняется (22), то прямые пересекаются; в случае не выполнения равенства (22) прямые скрещиваются.

Заметим, что во всех рассмотренных случаях взаимного расположения прямых можно вычислять угол между прямыми. Угол между прямыми определяется с помощью скалярного произведения их направляющих векторов:

(23)

Числитель взят по модулю для того, чтобы (как и для плоскостей) угол получался острым (в крайнем случае прямым).

Пример 6 . Выяснить взаимное расположение трёх прямых:

Решение . По данным уравнениям определяем опорные точки и направляющие векторы:

Легко заметить, что следовательно, прямые или параллельны или совпадают. Подставим координаты точки в уравнение - получили неверные равенства, следовательно, параллельны.

Возьмём и проверим условие (22):

, следовательно, скрещиваются.

Теперь проверим условие (22) для

следовательно, пересекаются.

5.7. Взаимное расположение прямой и плоскости в пространстве.

Прямая и плоскость в пространстве могут пересекаться и тогда возникают вопросы нахождения угла между прямой и плоскостью и координатах точки их пересечения. Прямая и плоскость могут быть параллельными, в частном случае, прямая лежит в плоскости. Рассмотрим все эти случаи.

Угол между прямой и плоскостью (см. рис. 8) определяется с

Помощью вектора нормали

Плоскости и направляющего вектора

Прямой: и направляющего вектора прямой что на плоскости (в двумерном направляющий вектор прямой, М (х, у) – произвольная точка прямой.Если в уравнении (32) раскрыть скобки и обозначить

уравнение прямой с опорной точкой и вектором нормали.

(36)

где общее уравнение прямой на плоскости.

Угол между двумя прямыми можно вычислять привычным для нас способом – с помощью скалярного произведения направляющих векторов прямых или их векторов нормали. Если две прямые заданы каноническими уравнениями

И т.е. направляющие векторы прямых, то (см. рис.10)

(37)

Уравнение плоскости. Как составить уравнение плоскости?
Взаимное расположение плоскостей. Задачи

Пространственная геометрия не намного сложнее «плоской» геометрии, и наши полёты в пространстве начинаются с данной статьи. Для усвоения темы необходимо хорошо разобраться в векторах , кроме того, желательно быть знакомым с геометрией плоскости – будет много похожего, много аналогий, поэтому информация переварится значительно лучше. В серии моих уроков 2D-мир открывается статьёй Уравнение прямой на плоскости . Но сейчас Бэтмен сошёл с плоского экрана телевизора и стартует с космодрома Байконур.

Начнём с чертежей и обозначений. Схематически плоскость можно нарисовать в виде параллелограмма, что создаёт впечатление пространства:

Плоскость бесконечна, но у нас есть возможность изобразить лишь её кусочек. На практике помимо параллелограмма также прорисовывают овал или даже облачко. Мне по техническим причинам удобнее изображать плоскость именно так и именно в таком положении. Реальные плоскости, которые мы рассмотрим в практических примерах, могут располагаться как угодно – мысленно возьмите чертёж в руки и покрутите его в пространстве, придав плоскости любой наклон, любой угол.

Обозначения : плоскости принято обозначать маленькими греческими буквами , видимо, чтобы не путать их с прямой на плоскости или с прямой в пространстве . Я привык использовать букву . На чертеже именно буква «сигма», а вовсе не дырочка. Хотя, дырявая плоскость, это, безусловно, весьма забавно.

В ряде случаев для обозначения плоскостей удобно использовать те же греческие буквы с нижними подстрочными индексами, например, .

Очевидно, что плоскость однозначно определяется тремя различными точками, не лежащими на одной прямой. Поэтому достаточно популярны трёхбуквенные обозначения плоскостей – по принадлежащим им точкам, например, и т.д. Нередко буквы заключают в круглые скобки: , чтобы не перепутать плоскость с другой геометрической фигурой.

Для опытных читателей приведу меню быстрого доступа :

• Как составить уравнение плоскости по точке и двум векторам?
• Как составить уравнение плоскости по точке и вектору нормали?

и мы не будем томиться долгими ожиданиями:

Общее уравнение плоскости

Общее уравнение плоскости имеет вид , где коэффициенты одновременно не равны нулю.

Ряд теоретических выкладок и практических задач справедливы как для привычного ортонормированного базиса, так и для аффинного базиса пространства (если масло - масляное, вернитесь к уроку Линейная (не) зависимость векторов. Базис векторов ). Для простоты будем полагать, что все события происходят в ортонормированном базисе и декартовой прямоугольной системе координат.

А теперь немного потренируем пространственное воображение. Ничего страшного, если у вас оно плохое, сейчас немного разовьём. Даже для игры на нервах нужны тренировки.

В самом общем случае, когда числа не равны нулю, плоскость пересекает все три координатные оси. Например, так:

Ещё раз повторю, что плоскость бесконечно продолжается во все стороны, и у нас есть возможность изобразить только её часть.

Рассмотрим простейшие уравнения плоскостей:

Как понимать данное уравнение? Вдумайтесь: «зет» ВСЕГДА, при любых значениях «икс» и «игрек» равно нулю. Это уравнение «родной» координатной плоскости . Действительно, формально уравнение можно переписать так: , откуда хорошо видно, что нам по барабану, какие значения принимают «икс» и «игрек», важно, что «зет» равно нулю.

Аналогично:
– уравнение координатной плоскости ;
– уравнение координатной плоскости .

Немного усложним задачу, рассмотрим плоскость (здесь и далее в параграфе предполагаем, что числовые коэффициенты не равны нулю). Перепишем уравнение в виде: . Как его понимать? «Икс» ВСЕГДА, при любых значениях «игрек» и «зет» равно некоторому числу . Эта плоскость параллельна координатной плоскости . Например, плоскость параллельна плоскости и проходит через точку .

Аналогично:
– уравнение плоскости, которая параллельна координатной плоскости ;
– уравнение плоскости, которая параллельна координатной плоскости .

Добавим членов: . Уравнение можно переписать так: , то есть «зет» может быть любым. Что это значит? «Икс» и «игрек» связаны соотношением , которое прочерчивает в плоскости некоторую прямую (узнаёте уравнение прямой на плоскости ?). Поскольку «зет» может быть любым, то эта прямая «тиражируется» на любой высоте. Таким образом, уравнение определяет плоскость, параллельную координатной оси

Аналогично:
– уравнение плоскости, которая параллельна координатной оси ;
– уравнение плоскости, которая параллельна координатной оси .

Если свободные члены нулевые, то плоскости будут непосредственно проходить через соответствующие оси. Например, классическая «прямая пропорциональность»: . Начертите в плоскости прямую и мысленно размножьте её вверх и вниз (так как «зет» любое). Вывод: плоскость, заданная уравнением , проходит через координатную ось .

Завершаем обзор: уравнение плоскости проходит через начало координат. Ну, здесь совершенно очевидно, что точка удовлетворяет данному уравнению.

И, наконец, случай, который изображён на чертеже: – плоскость дружит со всеми координатными осями, при этом она всегда «отсекает» треугольник, который может располагаться в любом из восьми октантов.

Линейные неравенства в пространстве

Для понимания информации необходимо хорошо изучить линейные неравенства на плоскости , поскольку многие вещи буду похожи. Параграф будет носить краткий обзорный характер с несколькими примерами, так как материал на практике встречается довольно редко.

Если уравнение задаёт плоскость, то неравенства
задают полупространства . Если неравенство нестрогое (два последних в списке), то в решение неравенства кроме полупространства входит и сама плоскость.

Пример 5

Найти единичный нормальный вектор плоскости .

Решение : Единичный вектор – это вектор, длина которого равна единице. Обозначим данный вектор через . Совершенно понятно, что векторы коллинеарны:

Сначала из уравнения плоскости снимем вектор нормали: .

Как найти единичный вектор? Для того чтобы найти единичный вектор , нужно каждую координату вектора разделить на длину вектора .

Перепишем вектор нормали в виде и найдём его длину:

Согласно вышесказанному:

Ответ :

Проверка: , что и требовалось проверить.

Читатели, которые внимательно изучили последний параграф урока , наверное, заметили, что координаты единичного вектора – это в точности направляющие косинусы вектора :

Отвлечёмся от разобранной задачи: когда вам дан произвольный ненулевой вектор , и по условию требуется найти его направляющие косинусы (см. последние задачи урока Скалярное произведение векторов ), то вы, по сути, находите и единичный вектор, коллинеарный данному. Фактически два задания в одном флаконе.

Необходимость найти единичный вектор нормали возникает в некоторых задачах математического анализа.

С выуживанием нормального вектора разобрались, теперь ответим на противоположный вопрос:

Как составить уравнение плоскости по точке и вектору нормали?

Эту жёсткую конструкцию вектора нормали и точки хорошо знает мишень для игры в дартс. Пожалуйста, вытяните руку вперёд и мысленно выберите произвольную точку пространства, например, маленькую кошечку в серванте. Очевидно, что через данную точку можно провести единственную плоскость, перпендикулярную вашей руке.

Уравнение плоскости, проходящей через точку перпендикулярно вектору , выражается формулой:

1. Можно доказать утверждение, что если в пространстве задана прямоугольная система координат ОХУZ, то всякое уравнение первой степени с тремя неизвестными х,у,z необходимо и достаточно определяет относительно этой системы некоторую плоскость Р . Уравнение это называется общим уравнением плоскости и имеет следующий вид:

Ах + Ву + Сz + D= 0 (17)

(сравните с общим уравнением (15) прямой на плоскости, которое следует из этого при z = 0) и определяет плоскость Р , перпендикулярную вектору (А,В,С).

Вектор - нормальный вектор плоскости Р .

Уравнению (17) эквивалентны следующие уравнения.

2. Уравнение плоскости, проходящей через заданную точку М(х 0 , у 0 , z 0 ):

А(х - х 0) + В(у -у 0) + С(z -z 0) = 0.

3. Уравнение плоскости в отрезках

,

где ; ; .

4. Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой, записывается в виде определителя

,

где (х 1 , y 1 , z 1), (х 2 , y 2 , z 2), (х 3 , y 3 , z 3) - координаты заданных точек.

Угол между двумя плоскостями определяется как угол между их нормальными векторами n 1 и n 2 . Отсюда условие параллельности плоскостей

Р 1 и Р 2:

и условие перпендикулярности двух плоскостей:

А 1 А 2 + В 1 В 2 + С 1 С 2 = 0 .

Пример 29 . Через точку К (1, -3, 2) провести плоскость, параллельную векторам

а = (1, 2, -3) и b = (2,-1,-1) .

Решение. Пусть М (х , у , z ) – произвольная точка искомой плоскости. Вектор

КМ = (х - 1, у + 3, z - 2) лежит в этой плоскости, а векторы а и b ей параллельны. Следовательно, векторы КМ , а и b – компланарны. Тогда их смешанное произведение равно нулю:

.

Отсюда -(х –1) - (у + 3) – 5(z – 2) = 0 или х+ 7у + 5z + 10 = 0. Это и есть искомое уравнение плоскости.

Различные виды уравнения прямой в пространстве

Прямую линию в пространстве можно задавать в виде:

1) линии пересечения двух не совпадающих и не параллельных плоскостей Р 1 и Р 2:

;

2) уравнения прямой, проходящей через данную точку М (х 0 , у 0 , z 0) в направлении, задаваемом вектором L = (m, n, p ):

,

которое называется каноническим уравнением прямой в пространстве;

3) уравнения прямой, проходящей через две заданные точки М (х 1 , у 1 , z 1)

и M (x 2 , y 2 , z 2):

;

4) параметрических уравнений:

.

Пример 30 . Привести к каноническому и параметрическому видам уравнение прямой

.

Решение. Прямая задана как линия пересечения двух плоскостей. Нормальные векторы этих плоскостей n 1 = (3,1,-2) и n 2 = (4,-7,-1) перпендикулярны к искомой прямой, поэтому их векторное произведение [n 1 , n 2 ] = L параллельно ей и вектор [n 1 , n 2 ] (или любой ему коллинеарный) можно принять за направляющий вектор L искомой прямой.

[n 1 , n 2 ] =
.

Примем за L = 3i + j + 5k . Остается найти какую-либо точку на заданной прямой. Положим для этого, например, z = 0. Получим

.

Решив эту систему, находим х = 1, у = - 2. Таким образом, точка К (1, -2, 0) принадлежит заданной прямой, а её каноническое уравнение имеет вид